티스토리 뷰
- 지금까지 배운거는 아래와 같다.
배치 정책 - 세그멘테이션, 페이징, 페이지드 세그멘테이션
가져오기 정책 - 디맨드 페이징
- 이번 글에서는 메모리가 꽉 찼을 때 어떤 페이지를 HDD 스왑 영역으로 보낼지 결정하는 페이지 교체정책을 알아보자
● 기본 개념
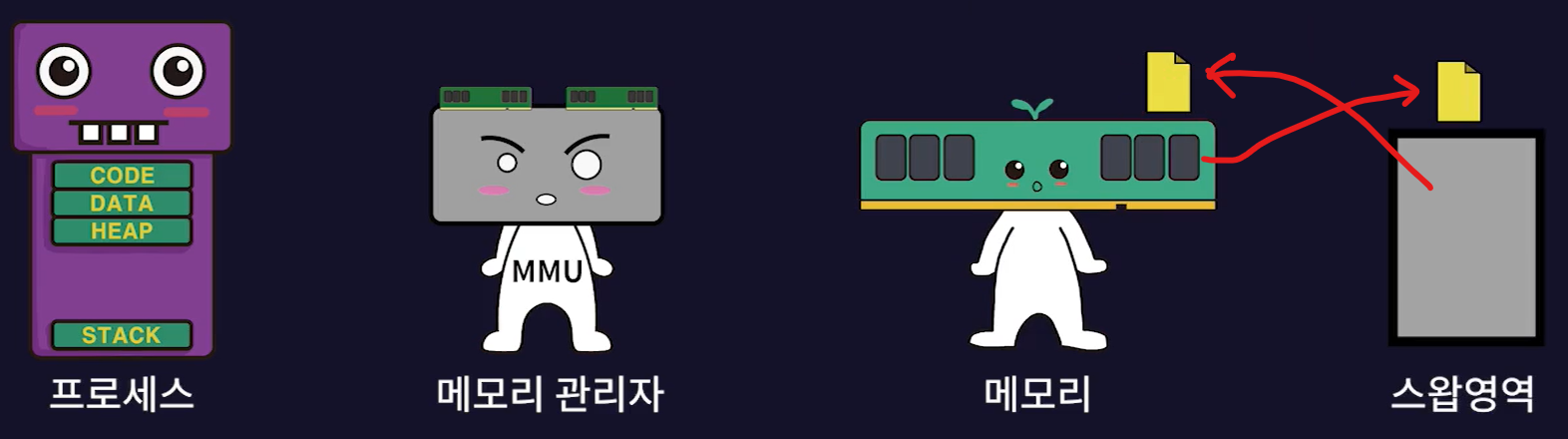
- 프로세스는 데이터 접근을 위해 메모리를 참조하는데 이때 원하는 데이터가 메모리에 없으면 Page Fault가 발생한다.
- Page Fault가 발생하면 해당 페이지를 스왑 영역에서 메모리로 불러와야 하는데 이때 메모리가 모두 차서 공간이 없다면 메모리에 있는 페이지 중 하나를 선택해서 스왑 영역으로 옮겨야 한다.
● 페이지 교체정책의 종류
- 메모리에 있는 페이지를 스왑 영역으로 옮길 때 어떤 페이지를 옮길지 결정하는 정책을 페이지 교체정책이라고 하며 여기에는 여러가지 방법이 있다.
1 Random
- 말 그대로 페이지를 무작위로 선택하는 방법이다.
- Random 방식은 지역성을 고려하지 않기 때문에 자주 사용되는 페이지가 선택될 때도 있어 성능이 별로 좋지 않다.
- 그래서 거의 사용되지 않는다.

2. FIFO(First In First Out, 먼저 들어온 놈이 먼저 나간다.) 알고리즘
- 메모리에 들어온지 가장 오래된 페이지를 선택하는 방법이다.
- 페이지 교체정책에서는 자주 쓰이는 페이지가 단순히 먼저 들어왔다는 이유만으로 교체되면 오히려 성능이 저하될 가능성이 있다.(컨텍스트 스위칭이 그 만큼 자주 발생하기 때문에)
- 이러한 단점에도 불구하고 FIFO 방식은 구현이 간단하고 성능도 어느정도 보장되기 때문에 변형을 한 형태로 많이 쓰인다.
- FIFO의 가장 큰 문제는 빌레이디의 역설이다.
- 빌레이디의 역설은 page fault를 줄이기 위해 메모리를 늘려 프레임 수를 늘렸는데 오히려 page fault가 더 많이 발생하는 현상이다.
- 빌레이디의 역설은 FIFO에서만 발생하며 LRU(Least Recently Used)에서는 발생하지 않는다.
3. Optimum 알고리즘
- 앞으로 가장 오랫동안 쓰이지 않을 페이지를 선택하는 방법이다.
- 그러나 해당 방법은 사실상 구현이 불가능한 이론적인 방법이라고 할 수 있다.(앞으로 누가 어떻게 얼마나 사용될지 알 수 없기 때문)
- Optimum 방식은 다른 알고리즘과 성능 비교를 할 때 참조용으로 쓰인다.
4. LRU(Least Recently Used) 알고리즘
- 최근에 사용 빈도가 가장 적은 페이지를 선택하는 방법
- 지역성 이론의 시간의 지역성에 따르면 최근 사용된 데이터(페이지)가 앞으로도 사용될 확률이 높으며 최근 사용을 가장 적게한 데이터(페이지)가 앞으로도 사용될 확률이 낮다.
- 이러한 개념이 있기에 LRU 알고리즘은 Optimum 알고리즘과 유사한 성능을 나타낸다. 단, 프로그램이 지역성을 띄지 않으면 성능이 떨어진다.
● FIFO, Optimum, LRU 비교
- FIFO, Optimum, LRU가 페이지를 교체하는 상황을 비교해 보자. 이때 페이지는 A, B, C, A, C, D, A, D, C, A, B 순서로 요청되는 상황이다.
- 참고로 page fault가 발생할 때마다 컨텍스트 스위칭이 일어나므로 그 만큼 성능이 떨어진다고 볼 수 있다.
1. FIFO, Optimum, LRU 모두 처음에는 메모리가 모두 비어있는 상황이므로 처음 A, B, C 요청에는 모두 page fault가 발생한다.


현재 남은 페이지 : A, C, D, A, D, C, A, B
2. 메모리에 A, B, C가 들어온 상태에서 그 다음 차례인 페이지 A에 대한 요청이 들어왔다.
- FIFO, Optimum, LRU 모두 현재 메모리에 페이지 A가 있기에 page fault가 발생하지 않는다.
현재 남은 페이지 : C, D, A, D, C, A, B
3. 그 다음 차례인 페이지 C에 대한 요청이 들어왔다.
- 역시 FIFO, Optimum, LRU 모두 현재 메모리에 페이지 C가 있기에 page fault가 발생하지 않는다.
현재 남은 페이지 : D, A, D, C, A, B
4. 그 다음 차례인 페이지 D에 대한 요청이 들어왔다.
- FIFO, Optimum, LRU 모두 현재 메모리에 페이지 D가 없기에 모두 page fault가 발생한다.


- Optimum은 이후 어떤 요청(A, D, C, A, B)이 있는지 전부 알고 있기 때문에 이를 훑어본 후 B가 가장 적게 사용된다는 것을 파악한다.
- 그렇기에 현재 메모리에 있는 페이지 B를 스왑 영역으로 옮긴 후 B가 있던 자리에 D를 가져다 놓는다.
- FIFO는 먼저 들어온 페이지가 먼저 나가기 때문에 페이지 A를 스왑 영역으로 옮긴 후 그 자리에 D를 가져다 놓는다.
- LRU는 최근에 가장 사용이 적은 페이지가 나가기 때문에 최근에 들어온 페이지의 참조 수를 계산한다.
- (A = 2번), (B = 1번), (C = 2번) 이므로 페이지 B를 스왑 영역으로 옮긴 후 B가 있던 자리에 D를 가져다 놓는다.
현재 남은 페이지 : A, D, C, A, B
5. 이런식으로 나머지 A, D, C, A, B 페이지가 들어오면 최종적으로 아래와 같은 모습이 된다.
- 이렇게 보면 LRU와 Optimum은 비슷하게 동작하는 것 같고 FIFO의 성능이 가장 좋지 않다.
- 그렇기에 LRU를 사용하는게 가장 최선의 방법처럼 보인다.

● LRU와 FIFO
- LRU를 구현하기 위해서는 시간을 기록해야 하는데 여기서 구현에 대한 어려움이 발생한다.
- 최근 가장 적은 사용을 파악해야 하는데 바로 그 최근이라는 시간을 다루는게 어렵다.
why? 시간을 기록할 bit가 많이 필요함은 물론 아무리 많은 bit가 있어도 시간이 아주 오래지난다고 하면 결국에는 오버플로우가 발생하기 때문이다.(오버플로우로 값이 초기화 되면서 시간을 올바르게 표현할 수 없게 된다.)
- 이 때문에 LRU와 유사하게 구현하는 방법을 고안했는데 이를 Clock Algorithm 이라고 한다.
cf) Clock Algorithm 보다 발전된 Enhanced Clock Algorithm도 있다.
Q. 그렇다면 LRU가 있으므로 FIFO를 사용하는 경우는 아예 없을까?
A. 그렇지 않으며 부득이하게 FIFO를 사용해야만하는 경우가 있다.
- LRU는 접근비트를 이용(by_Clock Algorithm)하는데 하드웨어적으로 접근비트를 지원하지 않는 시스템에서는 FIFO를 이용할 수 밖에 없다. 그렇기에 FIFO의 성능을 높이기 위한 방법도 있다.
- FIFO의 장점은 구현이 간단하다는 것인데 자주 사용되는 페이지가 교체될 수 있다는 단점이 있다.
- 이를 위해 2차 기회 페이지 교체 알고리즘을 고안했는데 말 그대로 FIFO 방식에서 자주 사용되는 페이지에게는 또 한 번의 기회를 주는 것이다.
- FIFO 방식과 동일하게 동작하지만 만약 page fault 없이 페이지 접근에 성공했다면 해당 페이지를 Queue의 맨 뒤로 이동시켜 페이지의 수명을 연장시켜주는 방식이다.
- 2차 기회 페이지 교체 알고리즘의 성능은 LRU 보다는 안 좋고 FIRO 보다는 좋다.
LRU 성능 > 2차 기회 페이지 교체 알고리즘 성능 > FIFO 성능

'CS > 운영체제' 카테고리의 다른 글
| #40 스레싱과 워킹셋 (0) | 2023.07.14 |
|---|---|
| #39 디맨드 페이징(가져오기 정책) (0) | 2023.07.13 |
| #38 페이지드 세그멘테이션(배치정책) (0) | 2023.07.12 |
| #37 페이징(배치정책) (0) | 2023.07.11 |
| #36 파일과 디스크 (0) | 2023.07.10 |
- Total
- Today
- Yesterday
- 빅데이터 분석기사
- node.js
- 코테
- 빅데이터
- OS
- API
- Phaser3
- 프로세스
- MySQL
- DART
- 코딩테스트
- jpa
- git
- Stream
- MongoDB
- Phaser
- 메모리
- SpringBoot
- 프로그래머스
- Advanced Stream
- nosql
- spring
- 운영체제
- 알고리즘
- java
- Spring Boot
- db
- SQL
- 자료구조
- Java8
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
