#11 삽입정렬(Insertion Sort)

● Insertion Sort?
- Insertion Sort 또한 어렵지는 않지만 성능이 아쉬운 정렬이다.
- Insertion Sort 또한 Selection sort와 마찬가지로 배열을 두 영역(정렬된 영역, 정렬되지 않은 영역)으로 나눠서 진행한다.
- Insertion Sort는 정렬되지 않은 영역의 가장 앞에 있는 데이터를 하나씩 꺼내서 정렬된 영역 내의 적절한 위치에 삽입해서 정렬하는 알고리즘이다.

[4, 1, 5, 3, 6, 2]

- 참고로 Insertion Sort는 첫 번째 원소(index = 0)는 이미 정렬이 되어있다는 가정하에 정렬을 하는 알고리즘이다.
- 아래 그림으로 보면 (index[0] = 4)는 이미 정렬되어 있는 상태이다.

출처 - 인프런, 그림으로 쉽게 배우는 자료구조와 알고리즘 (기본편)

1.
- 정렬되지 않은 영역의 첫 번째 원소인 (index[1] = 1)을 정렬된 영역에 삽입해 보자
- 삽입할 원소인 (index[1] = 1)과 정렬된 영역의 마지막 원소(index[0] = 4)를 비교한다.
cf) 지금은 정렬된 영역의 원소가 1개 이므로 (index[0] = 4)가 첫 번째이자 마지막 원소이다.

출처 - 인프런, 그림으로 쉽게 배우는 자료구조와 알고리즘 (기본편)

- (1 < 4)이므로 4를 오른쪽 인덱스(index[1])에 덮어씌운다.

출처 - 인프런, 그림으로 쉽게 배우는 자료구조와 알고리즘 (기본편)

- 이제 삽입할 데이터 1을 정렬된 영역의 또 다른 원소와 비교해야 하는데 더 이상 비교할 원소가 존재하지 않으므로 마지막에 비교한 4의 위치에 데이터 1을 '삽입'해준다.
- 이후 정렬된 영역과 정렬되지 않은 영역은 아래와 같다.

출처 - 인프런, 그림으로 쉽게 배우는 자료구조와 알고리즘 (기본편)

2.
- 정렬되지 않은 영역의 첫 번째 원소인 (index[2] = 5)를 정렬된 영역에 삽입해 보자
- 이를 위해서 정렬된 영역의 가장 뒤에 있는 원소부터 역순으로 비교한다.
- 현재 정렬된 영역의 가장 뒤에 있는 데이터는 (index[1] = 4)이므로 4와 5를 비교해보자
- (4 < 5)이므로 (index[2] = 5)가 현재 자리 그대로 있는게 올바르게 정렬된 모습이다.
- 이후 정렬된 영역과 정렬되지 않은 영역은 아래와 같다.

출처 - 인프런, 그림으로 쉽게 배우는 자료구조와 알고리즘 (기본편)

3.
- 정렬되지 않은 영역의 첫 번째 원소인 (index[3] = 3)을 정렬된 영역에 삽입해 보자
- 이를 위해서 정렬된 영역의 가장 뒤에 있는 원소부터 역순으로 비교한다.
- 현재 정렬된 영역의 가장 뒤에 있는 데이터는 (index[2] = 5)이므로 5와 3을 비교해보자
- (3 < 5)이므로 5를 오른쪽 index에 덮어씌운다.

출처 - 인프런, 그림으로 쉽게 배우는 자료구조와 알고리즘 (기본편)

- 삽입할 데이터 3을 조금 전에 비교한 5의 이전 데이터(= 4)와 비교해보자
- (3 < 4)이므로 4를 오른쪽 index에 덮어씌운다.

출처 - 인프런, 그림으로 쉽게 배우는 자료구조와 알고리즘 (기본편)

- 삽입할 데이터 3을 조금 전에 비교한 4의 이전 데이터(= 1)와 비교해보자
- (1 < 3)이므로 3을 1의 다음 index로 덮어씌운다.
- 이후 정렬된 영역과 정렬되지 않은 영역은 아래와 같다.

출처 - 인프런, 그림으로 쉽게 배우는 자료구조와 알고리즘 (기본편)

- 이러한 과정을 계속 반복하면 오름차순으로 정렬이 된다.

[1, 2, 3, 4, 5, 6]  -->  Insertion Sort이 끝난 모습

---

● 구현
- Insertion Sort는 첫 번째 원소(index = 0)는 이미 정렬이 되어있다는 가정하에 정렬을 하는 알고리즘이다.

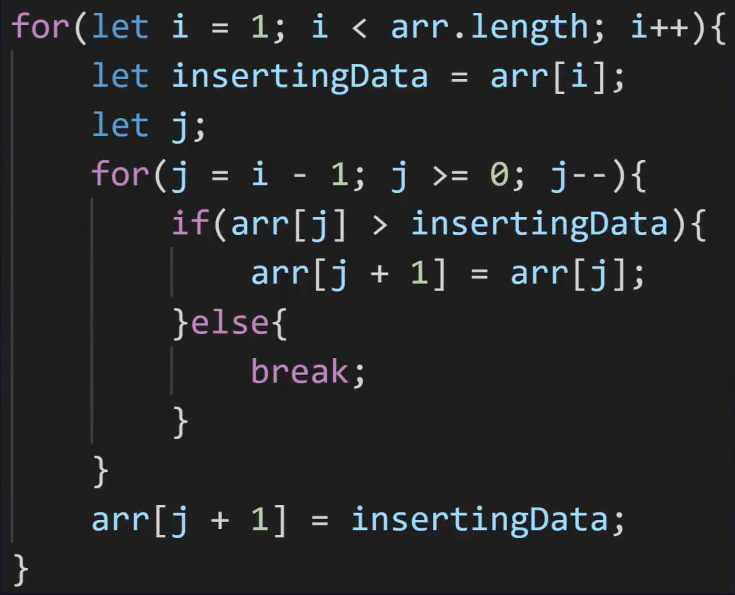
function insertionSort(arr) {
    // 정렬되지 않은 영역의 (첫 번째 원소 ~ 마지막 원소)를 순회하기 위한 for문
    for(let i = 1; i < arr.length; i++) {
        // 정렬 되지 않은 영역의 첫 번째 데이터(원소) = 삽입할 데이터
        let insertingData = arr[i];

        // 삽입 위치
        let j;

        // 정렬된 영역의 (맨 뒤 ~ 첫 번째 원소)를 역순으로 순회하며 삽입할 데이터의 위치를 찾는 for문
        for(j = (i - 1); j >= 0; j--) {
            if(arr[j] > insertingData) {
                // (현재 순회하는 인덱스의 원소 > insertingData)라면 순회하는 인덱스를 오른쪽 index에 덮어씌운다.
                arr[j + 1] = arr[j];
            } else {
                // insertingData 보다 작은 최초 원소를 발견했으니 for 문 종료
                // 그 이상은 비교해봤자 어차피 insertingData가 더 크다.
                // 삽입할 원소보다 작은 원소의 index는 현재 변수 j에 들어있는 상태이다.
                break;
            }
        }

        // j 보다 1 큰 위치에 insertingData 삽입
        arr[j + 1] = insertingData;
    }
}

let arr = [4, 1, 5, 3, 6, 2];

console.log("======= 정렬 전 =======");
console.log(arr);

insertionSort(arr);

console.log("======= 정렬 후 =======");
console.log(arr);

let i = 1
- Insertion Sort는 첫 번째 원소(index = 0)는 이미 정렬이 되어있다는 가정하에 정렬을 하는 알고리즘이므로
index[0] 원소는 굳이 순회할 필요없다.
- 반대로 말하면 (index = i)에 해당하는 원소는 아직 정렬이 되지 않은 영역의 첫 번째 데이터인 것이다.

let j = (i - 1)
- 정렬된 영역의 마지막 원소 = 정렬되지 않은 영역의 첫 번째 원소의 한 칸 앞
- 정렬되지 않은 영역의 첫 번째 원소는 i 이므로  j = (i - 1)로 선언해 정렬된 영역의 맨 뒤로 설정한다.

arr[j + 1] = insertingData;
- if(arr[j] > insertingData) --> 이 조건이 false가 된 것
- 즉, arr[j]의 바로 앞에 insertingData를 넣어야 한다는 의미이므로 +1 을 해줘야한다.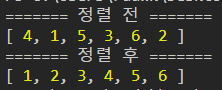

---

● Insertion Sort 성능과 장단점
- Insertion Sort도 Bubble Sort, Selection sort과 유사한 패턴의 for 문을 가지고 있다.
- 즉, Insertion Sort의 성능도 O(n^2) 이다.

출처 - 인프런, 그림으로 쉽게 배우는 운영체제

Insertion Sort	Insertion sort 단점
이해와 구현이 간단	성능이 O(n^2)으로 좋지 않다.